老年退役选手的复建之路
-
面试题 17.20. 连续中值
随机产生数字并传递给一个方法。你能否完成这个方法,在每次产生新值时,寻找当前所有值的中间值(中位数)并保存。
动态维护集合中的中位数,要求复杂度均摊O(logn)
首先这题平衡树肯定可以做,有没有更简单的办法呢?
设某个状态中位数已经求出来了为x,那么对于新加的元素:如果元素>x,则新中位数一定为x的后继;<x,为x的前驱,这点很显然
换言之我们只需要维护当前中位数的后继和前驱就好了,但是这个好像又涉及到平衡树了...
假设我们找到了x的前驱为y,那么我们必须要马上获得y的前驱...好消息是,我们不需要对<x的所有数排序,只需要每次获取最大值就行了,是不是很像堆?
所以我们维护一个大根堆和一个小根堆,大根堆维护<mid的数值,小根堆维护>mid的数值就好了,每次插入数字的时候将其与mid比较,当两个堆差值>2的时候及时平衡(就是把一个堆的顶部移到另外一个堆里就好)。面试题 17.19. 消失的两个数字
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
设缺的两个数字为a b
遍历第一遍可以把a+b找到,a一定<(a+b)/2
遍历第二遍把a找到就行了 -
看不懂,感觉很厉害
-
看的想学计算机
-
778 水位上升的泳池中游泳
二分答案+bfs793 阶乘函数后k个零
首先考虑到2*5=0且5的数量远小于2,不难发现F(x)实际上就是从1到x的数组中所有5的因数个数(当然我是打表之后强行总结的哈哈)。
那么第一个问题就是快速求F(x),x/5显然是1到x中能被5整除的个数,那么把这个数字再/5就是能被25整除的个数,这样递归一下就行,复杂度O(logN)。
之前的打表发现:凡是存在x,k使得F(x)=k,那么满足上式的x的数量一定为5,换句话说我们只要验证给定的k,是否存在某一个x即可。F函数显然单调,二分一下就行了。
复杂度两个log -
@xujing691691 希望你夺冠以后,不要忘记狠狠奖励自己。
-

k=2的时候就是传统区间dp,那么k>2的时候怎么做呢?
一个简单的思想就是记dp[i][j][k]为区间i-j中还剩k堆石子的最小代价,两个区间要么执行合并操作要么不合并石子单纯合并区间。然后思考之后发现第三维k也是多余的:dp[i][j]代表把i-j里面的所有石子合并到不能再分的最小堆数的最小代价,显然这个最小堆数是个定值。
转移的时候分类讨论两种情况:
1.不合并石子单纯合并两个区间,必须保证合并之后的石子堆数严格小于k
2.全部合并,必须保证合并之前两个区间的堆数总和为k典型的区间DP O(N^3)
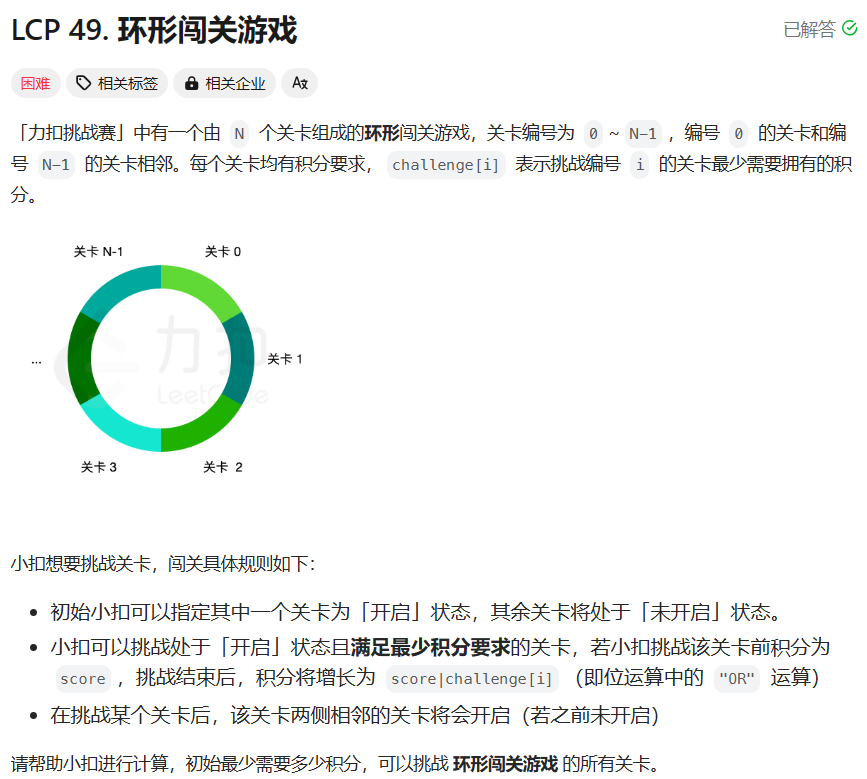
想法不算难但是细节很多的一道题
环形区间一般可以通过拉长到两倍长度当线段处理,然后这道题乍一看答案具有很强的单调性,那么简化之后的模型就是【给定一个初始积分x,问是否能填满整个线段】,朴素的暴力是O(N^2)的显然不行。
下一个想法就是初始将所有积分<=x的关卡都看为原点,然后暴力左右扩张合并,直到不能合并为止。合并的顺序也有说法,权值越大的点合并的顺序就尽量要越晚,考虑到区间1遇到一个障碍物p无法与区间2合并,之后p被消除,进行区间合并的时候,区间2显然可以无脑接受区间1中的所有顶点(权值一定<p),而反过来就不行了。
那就把整个环看成一张图做并查集,合并的时候还需要维护区间的左右界,总之细节不少。
那么就二分最终答案...交了最终代码之后发现答案错误,发现这个答案他并不具有单调性!因为或的原因可能存在下面一堆低位1可以通过但是上面一个高位1不能通过,那就把答案初始化赋值为全1,然后从高位到低位尝试删除1之后判断能不能通过,贪心一下就好。
复杂度O(nlogp),实际上logp就是long long的位数。

状压dp,dp[i][j]看作已经完成前i个位置的所有防护的同时,第i+1个位置的防护状态为j,j按照1-5秒压缩状态即可
-

不难发现某一行/一列中的棋子颜色排布只满足两种情况:
1.红/黑纯色
2.红黑一个一个交替爆搜出合法状态之后状压dp,每个位置有七种状态:
0-该位置之前未放置棋子
1/2-该位置之前放置过恰好一个红/黑棋子
3/4-该位置之前放置过多个红/黑棋子
5/6-该位置为红黑交替且最后一个位置恰好为红/黑色
树上按照dfs序一边处理子节点,获得路径之后按照字典序排序在子树树根递归合并
-
这几天要去面试了
-
@xujing691691 好好调整,等你请我吃华莱士
-
@xujing691691 gogogo鲸哥
-
找到班了
-
like